La maîtrise statistique des processus (MSP ou SPC - statistical process control) est l'un des principaux outils de la démarche 6-sigma. Elle s'intègre également dans le pilier JIDOKA (bon du premier coup) de l'approche Lean dans la mesure où elle permet de réduire la variabilité du processus de production.
L'objet de la MSP est de donner aux opérateurs de machines de production un outil graphique simple de pilotage de la production (il s’agit d’autocontrôle) leur permettant de maintenir la production centrée sur sa cible et de maintenir sa dispersion à l'intérieur de l'intervalle de tolérance spécifié (IT).
La MSP s'appuie sur deux outils fondamentaux:
· le suivi des processus par « cartes de contrôle » (créées par W. Shewhart, dès 1930) et
· la mesure des capabilités des moyens de production (développée à partir des années 1970).
Adaptée aux productions en série, la MSP reste pertinente également pour les productions en très petites séries voire unitaires (l'effet de série pourra être rétabli en calculant une moyenne glissante des valeurs individuelles).
Les cartes de contrôle
Les cartes de contrôles permettent de piloter la production (régler les consignes appliquées aux machines) par rapport aux limites naturelles du processus (il s’agit de la dispersion du moyen de production autour de sa consigne en l’absence de cause particulière de déréglage) et non par rapport aux spécifications (intervalle de tolérance défini par la tolérance supérieure, TS et la tolérance inférieur, TI), qui servent seulement à accepter ou non une production.
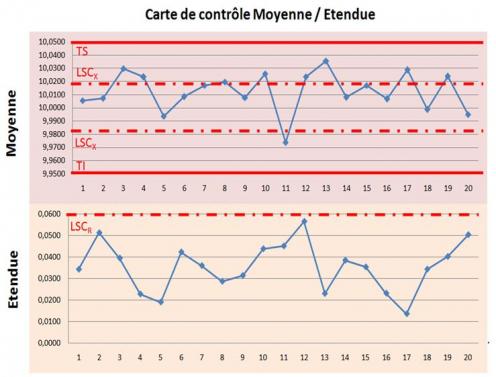
Un pilotage aux tolérances consistant à régler une machine uniquement lorsque la cote d’une pièce sort de l’intervalle de tolérance conduit, en effet, à appliquer des réglages trop tardivement (des rebuts ont déjà été produits) ou à tort (alors que la machine est en fait centrée).
Ainsi, même pour une production soumise à un tri à 100%, les cartes de contrôle restent pertinentes: le tri permet d'écarter les pièces non conformes alors que les cartes de contrôle permettent d'éviter de produire des pièces non conformes !
Le suivi de production par cartes de contrôle consiste à prélever, à fréquence constante, un échantillon de pièces dont on mesure la caractéristique qui fait l’objet du suivi (généralement une cote): l’opérateur calcule alors la moyenne et l’étendue de chaque échantillon qu’il reporte sur une carte afin de les comparer aux limites naturelles du processus. Lorsque ces valeurs « sortent » des limites, l’opérateur sait que le processus fait l’objet d’une cause spéciale (un déréglage, un défaut de lubrification, un outil usé,...). Il doit, alors, prendre l’action corrective qui va permettre de recentrer le processus sur sa cible, à l’intérieur de l’intervalle de tolérance.

