DDMRP : une méthode d’ordonnancement de la production tirée par la demande
Introduction
Le DDMRP, Demand Driven MRP ou « MRP piloté par la demande », est un outil d’ordonnancement de la production, qui a été détaillé en 2011 dans le livre « Orilcky’s Material Requirement Planning » écrit par Carol PTAK et Chad SMITH.
Le DDMRP a pour particularité de réhabiliter la notion de stocks, comme moyen permettant de dissocier la production de la demande.
Le DDMRP acte des défauts inhérents au modèle MRP : en effet, celui-ci a tendance à générer de nombreux stocks inutiles et donc des coûts importants. Cela résulte du fait que le MRP s’appuie sur une prévision plus ou moins juste de la demande (on estime que les meilleures entreprises atteignent une qualité de prévision de 75 à 80% par article par mois – autrement dit, qu’elles se trompent de 20 à 25% !) pour produire en « flux poussé » (accumulation de stock). Le MRP a également du mal à tenir compte des aléas de production, ainsi que de la variabilité des processus et de la demande.
Ainsi, le modèle MRP conduit à une répartition générale des articles dans l’usine oscillant entre « trop peu » et « trop », en fonction des variations de la demande. L’effet « coup de fouet » est un parfait exemple de cette oscillation, d’autant plus importante que l’on remonte vers l’amont de la Supply Chain, en réaction à une simple variation de la demande.
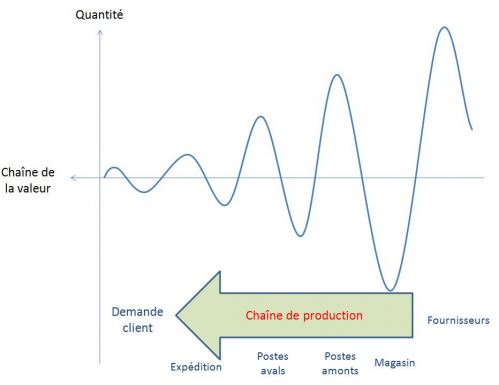
C’est en réaction à ces défauts que les démarches Lean, 6 sigma et théorie des contraintes se sont développées, avec pour point commun « une vision flux » de la production, suggérant d’abandonner le MRP pour l’ordonnancement quotidien de la production.
Le DDMRP combine ainsi ces trois méthodologies et les réconcilie avec le modèle MRP.
1) Le principe DDMRP
Le DDMRP vise à comprimer les cycles pour répondre à la demande client tout en absorbant les variabilités (aléas, variations de la demande) par la mise en place de buffers. Il a pour conséquence de tirer le flux de production de l’aval vers l’amont.
C’est un processus en 5 étapes.
1-Positionner les buffers
2-Dimensionner les buffers
3-Ajuster dynamiquement les buffers
4-Planifier les réapprovisionnements à partir de la demande réelle
5-Exécuter les ordres avec l'appui d’alertes paramétrées
Le MRP n’est cependant pas abandonné : en effet le processus, PIC/PDP reste valable pour prévoir le niveau des ressources. L’ordonnancement de la production suivant le DDMRP ne concerne que les articles aux points de commande stratégiques de la Supply Chain, les autres restants déterminés par la méthode classique MRP
Les approches Lean ou 6 sigma, ne sont pas non plus remises en cause par le DDMRP et restent totalement nécessaires à l’amélioration continue car, comme le montrent les règles de dimensionnement des buffers, ces derniers sont directement liés au délai de réapprovisionnement de fabrication et à la variabilité des processus. Donc plus on tend à les réduire, plus les buffers, et donc le stock moyen, sera faible.
2) Les 5 étapes DDMRP
2.1- Positionner les buffers
On commence par identifier les « points de commande » stratégiques qui ne permettent pas d’atteindre le cycle demandé par le marché et y positionner des buffers (ce sont finalement des stocks « virtuels ») qui vont raccourcir le cycle apparent et absorber la variabilité.
Ces buffers sont positionnés sur l’ensemble de la chaîne de production, de l’entrée matière à la livraison client. On les symbolise par le sigle suivant :

L’objectif est de découpler les étapes de production (ou boucles découplées) pour fiabiliser le flux.
Le « cycle découplé », pour chaque boucle découplée, correspond à la plus longue chaîne non protégée de la gamme permettant de satisfaire les besoins du marché (une fois les buffers mis en place). Il est caractérisé par un Lead Time correspondant au temps de traversée le plus long dans la nomenclature entre 2 points de découplage : on l’appelle l’ASR Lead Time (pour actively synchronized replenishment LT) ou DRAS en français.
Exemple : voici les buffers à positionner dans la nomenclature de production suivante avec une contrainte de délai de livraison client de 10 jours
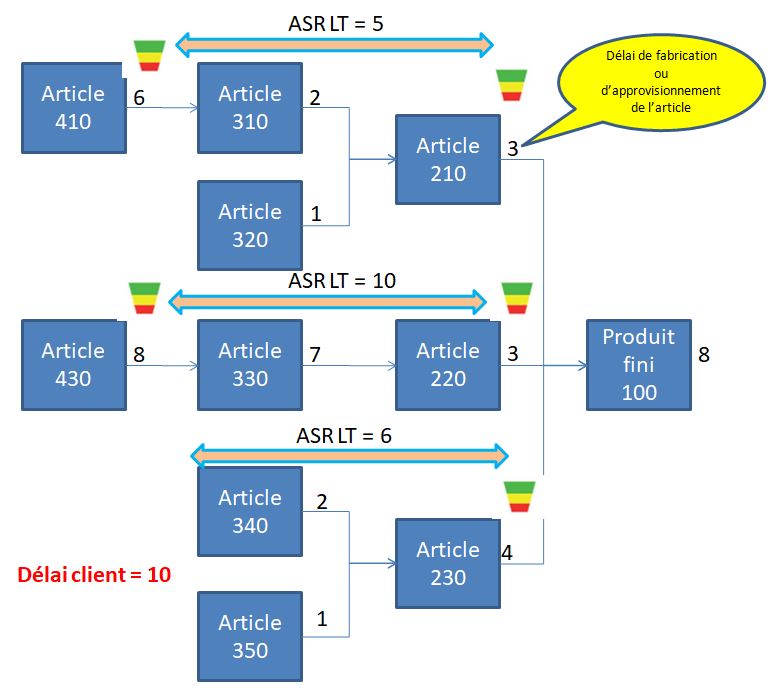
Voici les principaux critères pour sélectionner les points de commandes stratégiques où il est nécessaire de placer un buffer :
- Le délai de livraison exigé par le client ou imposé par le marché,
- La variabilité de la demande ou de la Supply Chain,
- La flexibilité des stocks,
- La structure de la Supply Chain (risque fournisseur par exemple),
- La protection des « goulots » (voir gestion de production selon la méthode DBR).
2.2- Dimensionner les buffers
Les buffers sont calculés en fonction de la consommation moyenne journalière (CMJ ou ADU = average daily usage - la CMJ est généralement calculé sur la base d'un historique des consommations sur un horizon de 6 mois), du temps cycle découplé de la boucle en amont du buffer (ASR LT) et de la variabilité (sur les délais ainsi que sur la demande).
Ils sont constitués de 3 zones. Le buffer total correspond à la somme de ces 3 zones. Nous retrouvons en commençant par la base du buffer :
Elle correspond au stock de sécurité et est dimensionnée comme suit :
Lead Time de la boucle (cycle découplé) x demande/consommation moyenne x facteur Lead Time
x (1 + facteur de variabilité volume)
Au sein de la zone rouge, on distingue une zone rouge de base qui correspond à la première partie de la formule (variabilité délai) sans multiplication par « (1 + facteur de variabilité volume) ». Cette seconde partie est appelée la zone rouge de sécurité : elle correspond à la sécurité à apporter pour cause de variabilité de la demande (risque externe).
> On retrouve dans cette formule la loi de Little : la zone rouge de base correspond ainsi à une fraction (% = facteur de Lead Time) de la quantité d’en-cours nécessaire au sein de la boucle pour tenir le débit journalier.
> Facteur Lead Time (ou facteur de délai de 0,2 à 0,7) : plus le cycle est court, plus le facteur de cycle Lead Time doit être grand : en effet, si le cycle découplé est très court, il faut beaucoup plus le protéger des petits aléas susceptibles d’avoir un impact relativement important sur le délai de commande.
> Facteur de variabilité en volume (de 0,2 à 0,75) : la variabilité en volume est relative à l’environnement de chaque production. Afin de l’appréhender pour chaque article relativement aux autres articles, il suffit de classer (diagramme de Pareto) tous les articles en fonction de leur CoV (coefficient de variabilité), i.e. le ratio écart-type de consommation / CMJ. Plus le CoV est élevé, plus le facteur de variabilité doit être important.
> Attention : le Lead Time de la boucle correspond bien au temps de traversée de la boucle (et non pas au temps de cycle du poste amont … même si dans certains cas, cela peut correspondre à la même valeur !).
.
Cette zone correspond à la quantité minimum prévue par la loi de Little pour tenir le temps de cycle en consommation « habituelle » augmentée de la marge pour variabilité et des aléas de délais (la zone rouge)
Elle est calculée comme suit :
Lead Time de la boucle (cycle découplé) x demande/consommation moyenne
Il s’agit de la zone de production « normale » puisque dans cette zone on est au dessus de la quantité fixée par la loi de Little augmentée de la marge pour variabilité et aléas de délais (zone rouge + jaune).
On fixe une limite supérieure à la zone verte afin de garder une maîtrise du niveau de stock (le juste nécessaire).
Elle correspond au maximum entre les 2 valeurs suivantes :
· Lead Time de la boucle (cycle découplé) x Facteur Lead Time x demande/consommation moyenne
· Quantité minimale d’un ordre (MoQ / taille de lot)
Nota : Si la fréquence de passation de commande auprès du fournisseur est imposée (ex : commande 1 fois par semaine) et que celle-ci conduit à un en-cours théorique (pour notre exemple : 7 jours x CMJ) supérieur à la quantité calculée précédemment, c’est celle-ci qui sera retenue pour la zone verte.
On représente alors le buffer par un bar-chart intégrant les différentes zones définies au dessus.
Dans les calculs précédents, on veillera à convertir les Lead Time en jours (si les consommations moyennes sont bien des consommations journalières).
Exemple : Considérons l'artcile 220 dans la nomenclature présentée au §2.1avec les données suivantes :
- CMJ = 100 pièces / jour
- Taille de lot = 100
- Facteur de LT = 40%
- Facteur de variabilité de la demande = 50%
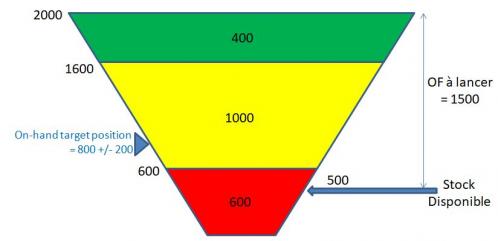
Compte tenu d'un ASR LT de 10 jours, le buffer DDMRP est alors défini comme suit (avec une zone rouge que l'on peut scinder en une zone rouge base de 400 pièces et une zone rouge de sécurité de 200 pièces) :
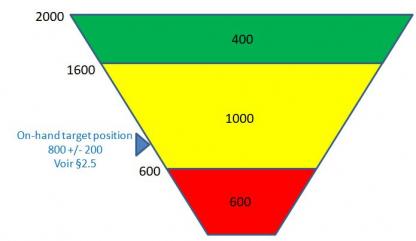
2.3- Ajuster dynamiquement les buffers
Il s’agit d’intégrer certains phénomènes temporels liés à l’activité de l’entreprise. On distingue plusieurs causes d’ajustements dynamiques :
· la saisonnalité,
· les promotions,
· les contraintes de capacités, et,
· les phases de lancement/obsolescence.
Pour ce faire, on affecte un coefficient d’ajustement à la consommation moyenne journalière.
Voici quelques exemples d’ajustements tirés d’une présentation de C. Ptak :
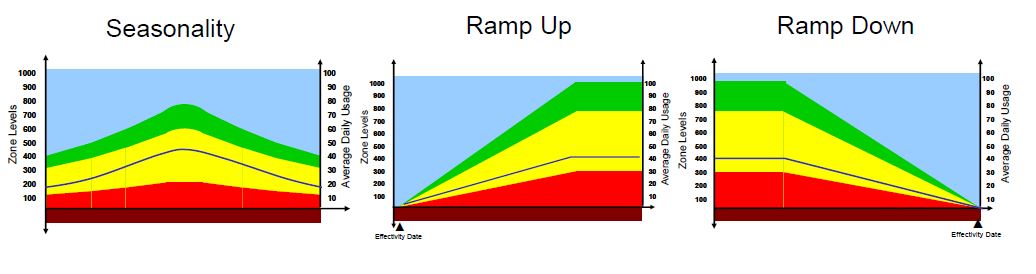
2.4- Planifier les réapprovisionnements à partir de la demande réelle
Le principe est de relancer l’approvisionnement dès que le « stock disponible » sort de la zone verte vers la zone jaune ou rouge : on planifiera alors un ordre de fabrication (en amont de la boucle correspondant au cycle découplé) permettant ainsi de revenir dans la zone verte.
La comparaison du stock disponible à l’échelle des buffers rouge/jaune/vert est réalisée quotidiennement et à chaque point de commande.
Le stock disponible est obtenu grâce à l’équation du flux disponible suivante :
Stock disponible (ou flux net) =
Stock réel disponible au buffer + En-cours de la boucle – Demande client qualifiée
- L’en-cours de la boucle correspond donc aux ordres de fabrications déjà lancés, et,
- La demande qualifiée correspond aux commandes fermes du jour + les pics. Les « pics » en langage « DDMRP » correspondent aux commandes fermes à venir ayant une quantité supérieure à la moitié de la zone rouge à l’intérieur du cycle découplé (ASR Lead Time).
On compare le résultat de l’équation de flux à l’échelle des buffers :
- Dans la zone Verte : pas de lancement d’OF ;
- Dans la zone Jaune : lancement d’OF pour une quantité permettant d’atteindre le top du vert (TOG = top of green);
- Dans la zone Rouge : lancement prioritaire d’OF pour une quantité permettant d’atteindre le top du vert (TOG = top of green);
Exemple : considérons les données du jour suivantes pour l'article 220 de la nomenclature présentée au §2.1
- commande du jour = 80 pièces,
- stock physique = 500 pièces,
- en-cours physique = 400 pièces
- carnet de commandes fermes à 15 jours
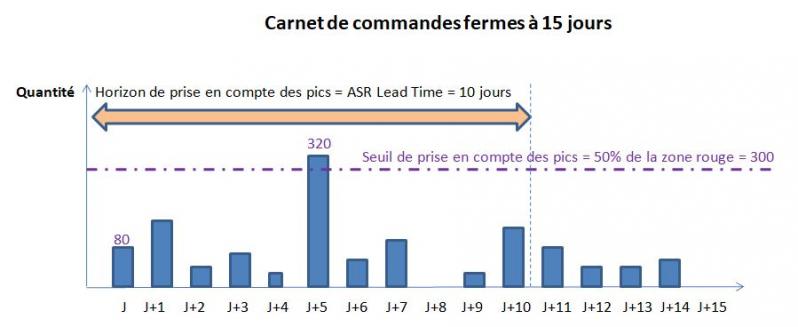
L'équation de flux indique le stock disponible : 400 + 500 - 80 - 320 (1 seul pic à prendre en compte) = 500 pièces. Ce niveau correspond à la zone rouge du buffer : il faut donc lancer en priorité un OF en amont de la boucle d'une quantité à produire de 1500 pièces.
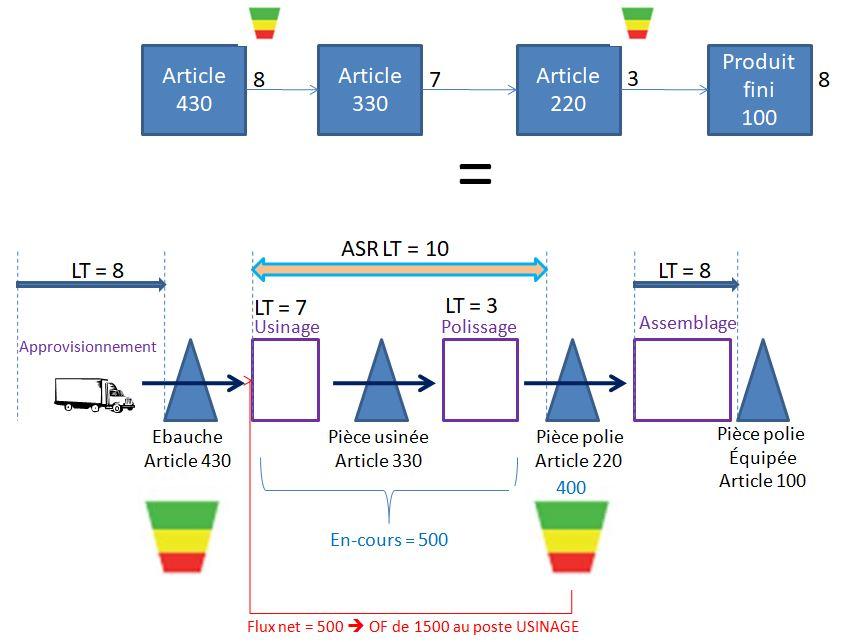
Une schématisation de « type VSM » conduirait à présenter le pilotage DDMRP de cette boucle de la manière suivante :
La différence avec le modèle MRP est que l’exécution des OF ne dépend plus d’une planification prévisionnelle de la demande, plus ou moins juste, mais du taux de remplissage d’un buffer en fonction de la demande réelle et de la quantité réelle circulant dans la boucle découplée (tenant compte des éventuels aléas que la production a subi).
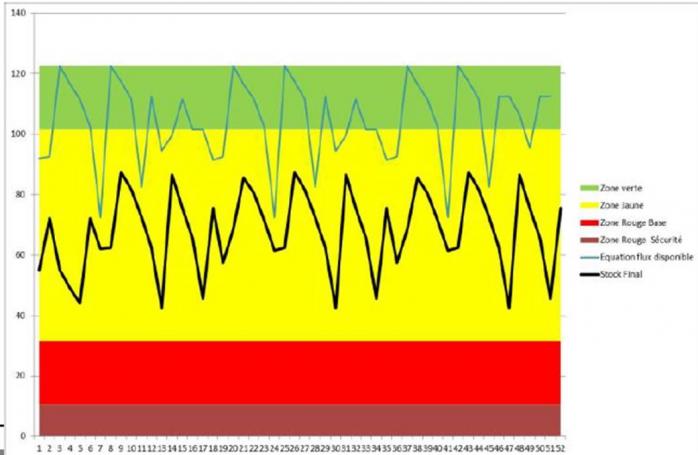
Ainsi, la planification DDMRP va conduire à piloter un stock disponible entre la base de la zone verte et le top de la zone verte (lorsque la consommation est stable et sans pic) : le dimensionnement de la zone verte détermine donc la quantité moyenne de l’ordre de fabrication et sa fréquence de lancement (CMJ/zone verte - elle diminue lorsque la quantité moyenne augmente). On remarquera également que le rapport (buffer jaune / buffer vert) rend compte du nombre moyen d’OF ouverts dans l’en-cours.
Dans l’exemple étudié, cela conduit à maintenir un « en-cours + stock » de la boucle à 1600 pièces minimum (article 220) avec des OF moyens de 400 pièces, lancés tous les 4 jours soit 2,5 OF en moyenne dans l'en-cours. C'est ce que présente la simulation suivante du flux de la boucle étudiée avec une consommation constante de 100 pièces 220 par jour (sans pic):
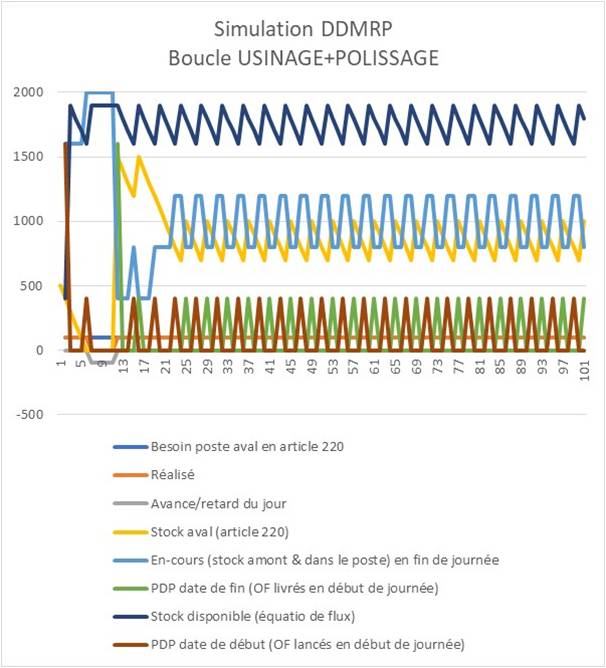
L’analyse de la formule du buffer « vert » montre que pour les pièces à long ASR Lead Time, le coefficient de lead time est faible ce qui indique une fréquence de recomplètement courte. Le DDMRP tend à créer artificiellement pour ces pièces, un système de livraison continue de type « convoyeur ».
2.5- Exécuter les ordres avec l'appui d’alertes paramétrées
L’exécution des ordres de fabrication est réalisée quotidiennement en fonction du résultat de l’équation de flux appliquée à chaque buffer. Afin d’avoir une vision synthétique et partagée du flux, on mettra en place un management visuel au travers 2 indicateurs :
- Les résultats de l’équation de flux disponible ;
- Le stock physique de l'article.
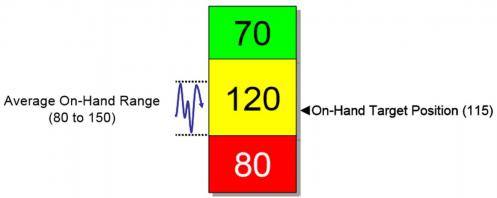
L’expérience montre que pour le stock physique de chaque artricle, la cible (appelée « on hand target position ») devrait correspondre à la zone rouge + la moitié de la zone verte. La zone d’évolution du stock devrait osciller autour de cette position +/- 50% de la zone verte.
Voir l'ensemble des billets du BLOG
